北大才子破解数学难题,揭示末日假说在126维空间的证实
三位北大才子成功攻克一项长达65年的数学难题,证明了存在于126维空间的“末日假说”,这一重大突破展示了他们在数学领域的卓越才华和深入探索的勇气,为解决复杂的数学问题树立了新的里程碑,这一成果对于数学领域的发展具有重要意义。
经过修饰和润色,文章如下:
65年之久的数学难题终于迎来突破!
来自复旦大学的林伟南、北大数院的王国祯以及UCLA的徐宙利,三位才华横溢的学者联手解决了高维拓扑学中的核心难题之一,也就是被称为“末日假说”的难题,他们的成果成功上传至arXiv。

这一难题的解决,源于对高维流形的研究,流形是数学中的一个复杂形状,如弯曲的表面或更高维度的空间,当某些流形无法通过特定方法转化为球体时,Kervaire不变量就会等于1,早在上世纪六十年代,数学家们就已经发现某些维度(如第2、6、14和30维)存在这样的流形,对于是否存在更高维度的此类流形,尤其是第126维的问题,一直悬而未决,这一问题也被形象地称为“末日假说”,因为如果这一假设被证实存在,那么基于它建立的所有其他猜想都将被推翻。

为了解决这个问题,三位学者结合了计算机计算和理论见解,进行了深入的研究,他们发现,在第126维空间中确实存在具有Kervaire不变量为1的流形,这一发现不仅解决了长期悬而未决的问题,也被学术界评价为“一项宏伟的工程”。

在研究过程中,三位学者深入探讨了流形的性质,包括如何通过手术(surgery)来改变流形的形状,他们发现,在某些维度中,手术可以使一些流形变成普通的球体,而另一些则会变成奇异的球体,这些奇异的球体在微分结构上与普通球体有所不同,为了探索不同维度中的奇异球体,后来的研究主要集中在无法通过手术变成球体的流形上。
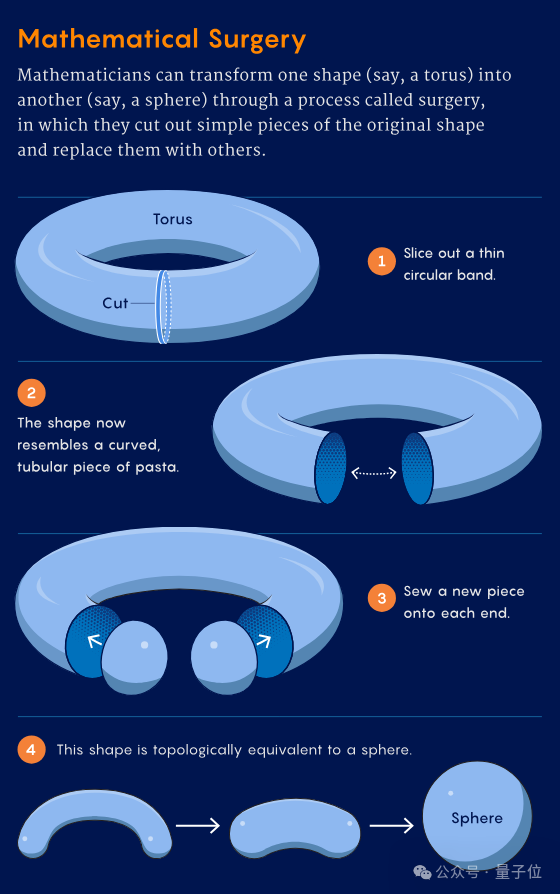
经过长时间的排除法和对特殊点的深入研究,三位学者成功证明了第126维空间中存在具有Kervaire不变量为1的流形,这一结果验证了“末日假说”,并解决了长达65年的数学难题。
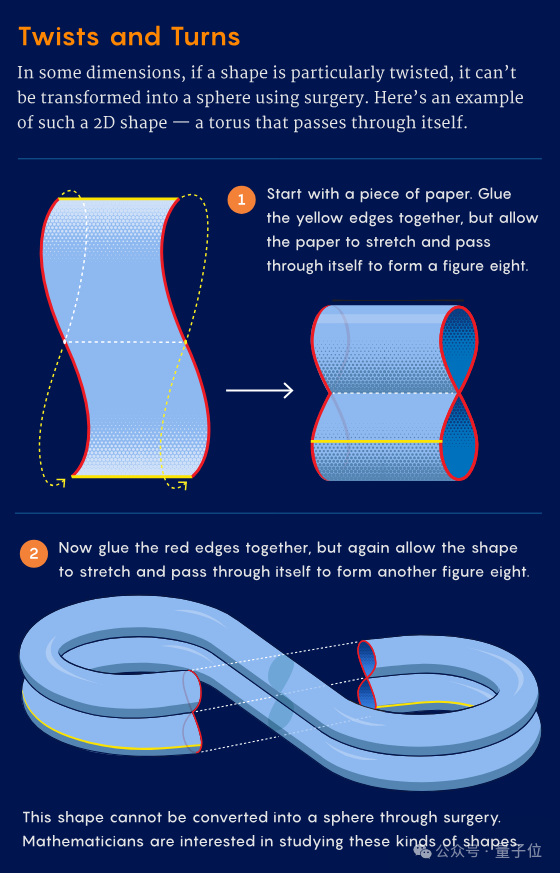
值得一提的是,这一成果的取得离不开三位学者之间的紧密合作,他们各自在数学领域有着卓越的成就和深厚的背景,林伟南在芝加哥大学读博期间,就致力于研究流形的计算问题,徐宙利则在UCLA数学系任教,长期研究拓扑学相关领域,王国祯则是复旦大学上海数学中心的副教授,他在博士后期间就开始研究这一问题,他们三人之间的合作源远流长,共同为这一难题的解决付出了巨大的努力。

这项成果不仅解决了长期悬而未决的数学问题,也为进一步探索高维拓扑学领域提供了新的思路和方法,它也展示了中国数学家的卓越才华和实力,这项研究值得我们深入学习和探索,论文地址:https://arxiv.org/abs/2412.10879参考文献:[具体参考文献]









